자료구조 공부(0) hash

아래 포스트는 Data Structure and Algorithmic Thinking with Python을 참고하여 작성되었습니다.

다른 자료구조부터 공부하려고했는데 hash얘기를 먼저 듣게 되어서 공부하게되었습니다.

Hashing is a technique used for storing and retrieving information as quickly us possible. It is used to perform optimal searches and is useful in implementing symbol tables

Why Hashing?

we saw that balanced binary search trees support operations such as insert, delete and search in O(logn) time. In applications, if we need these operations in 0(1), then hashing provides a way. Remember that worst case complexity of hashing is still 0(n), but it gives 0(1) on the average.

한정된 양의 해시테이블로 많은 값들을 저장할 수 있으며, 빠르게 찾을 수도 있다는 말입니다.

이러한 방식을 쓰는 이유는 간단합니다.

예를 들어서, 문자열에서 처음 반복되는 문자를 찾는 문제를 생각해봅시다.

만약 Brute-force 방식을 사용해서 이전까지의 문자들과 현재 문자를 비교한다면 시간복잡도는 O(n^2)가 될 것입니다. 그 대신에, 256 size의 0으로 초기화된 배열 arr을 사용해서

arr[ord(str[i])] += 1

을 지속적으로 시행하고, arr의 값이 2인 인덱스가 등장한다면, 그것이 최초로 반복되는 문자열인것으로 생각가능합니다.

그런데 Array의 한계점도 존재하는데, 이런 특수한 문제가 아니라 가능한 key들의 공간이 무한하다면(ex: 반복되는 문자 대신에 문자열을 찾는 문제) 이러한 방식으로 초기화할 수는 없을 것입니다.

그래서 한정된 공간을 잘 이용하기 위한 대안으로 hash function이 있습니다.

hash function은 f(key) = index로 대응되는 함수를 말하는데요

당연히 이상적으로는 f가 일대일함수이면 좋겠지만, 일반적으로 공역의 크기가 정의역보다 작기 때문에 일대일 함수를 만들 수 없습니다.

그렇기 때문에 같은 index에 저장되는 key값들이 많아질 수 밖에 없으며, 그것을 hash collision(해쉬 충돌)이라고 합니다.

좋은 맵핑을 만들기 위해서는 number of collision(동일한 맵핑)을 줄이는 것이 목적이며, 그것은 곧 hash table에 각 원소들이 동등한 비율로 분배되어야 함을 의미합니다.

일반적으로 그것을 달성하기 위한 방법이 몇가지 있습니다.

예) folding method

원소들을 동일한 크기의 조각들로 나눠서 생각.

원소에 대한 hash value값을 조각들의 hash value값들에 대한 함수로 나타내는 방식이다.

예를 들어서, 전화번호 436-555-4601을 2개씩 나누면 (43,65,55,46,01)이 된다.

43+65+55+46+01 = 210이 되는데, 만약 우리가 11개의 슬롯만 가지고 있다면, 11에 대한 modulo로 맵핑시키면 좋을 것이다.

꼭 이 방식만 되는 것은 아니며, 다양하게 도출할 수 있다.

A good hash function should have the following characteristics

• Minimize collision

• Be easy and quick to compute

• Distribute key values evenly in the hash table

• Use all the information provided in the key

4가지 모두 상식적으로 이해할 수 있을 법한 조건들이다.

저는 그 중에서 특히 2번째, Be easy and quick to compute가 중요하다고 생각하는데요,

예를 들어서 라빈-카프 알고리즘에서 Rabin fingerprint를 hash function으로 사용한다면, 계산시간을 매우 줄일 수 있습니다.

Collision Resolution Techniques

결론적으로 충돌이 일어나는 것은 막을 수 없으며, 우리는 충돌을 잘 해결하는 것이 관건입니다.

충돌이 일어난다고 데이터를 삭제하면 큰 문제가 일어나므로

그것을 위한 몇 가지 테크닉이 있다.

1. Direct chaining(Separate chaining)

   여러 collision이 나타난다면, 그러한 정보를 linked-list로 만들어서 이어보는 것이다.

   

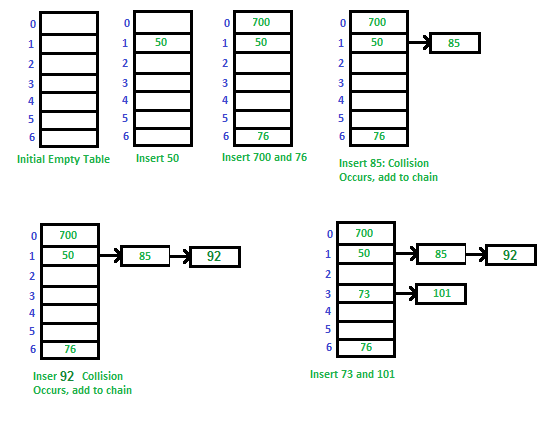
   Advantages: 1) Simple to implement. 2) Hash table never fills up, we can always add more elements to chain. 3) Less sensitive to the hash function or load factors. 4) It is mostly used when it is unknown how many and how frequently keys may be inserted or deleted.

   Disadvantages: 1) Cache performance of chaining is not good as keys are stored using linked list. Open addressing provides better cache performance as everything is stored in same table. 2) Wastage of Space (Some Parts of hash table are never used) 3) If the chain becomes long, then search time can become O(n) in worst case. 4) Uses extra space for links.

   매우 직관적이므로 많이 쓰이는데 단점도 있다고함.

   역시 연결리스트의 단점과 많이 연관되는 듯 합니다.

2. Open Addressing

   링크에 잘 설명되어 있는 것 같습니다.

   chain으로 연결하는게 아니라, 한 버킷당 들어갈 수 있는 엔트리가 하나뿐인 해시테이블입니다.

   

   이렇게 꼭 지정된 위치에만 원소가 들어가있는게 아니기때문에 선형탐사와 제곱탐사와 같은 방식(probing)을 통해서 키값을 찾아내야한다고 합니다.

라빈-카프 알고리즘

위에서 언급한 라빈-카프 알고리즘은 패턴매칭을 해결하는 알고리즘입니다.

(엄청 긴 문자열 S에서 패턴 P와 일치하는 부분을 찾는 문제)

일반적으로 이 문제를 Brute-force하게 푼다면 시간복잡도상 큰 문제가 발생하므로, 다른 방식이 필요합니다.

그 중 하나가, 라빈 카프 알고리즘인데, 로직은 간단합니다.

1. 각 string을 숫자로 맵핑하는 해시함수(Rabin fingerprint)를 만든다.
2. S[idx:idx+len(P)]와 P의 해시값을 비교하면서, 해시값이 일치하다면 단순비교를 한다.
3. 해시값이 다르거나, 단순비교가 안된다면 idx = idx+1

Rabin-fingerprint

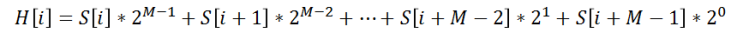
H[i] : 문자열의 해시함수값

S[i] : 각 문자의 아스키코드값

Rabin-fingerprint는 이런 좋은 성질을 가지고 있습니다.

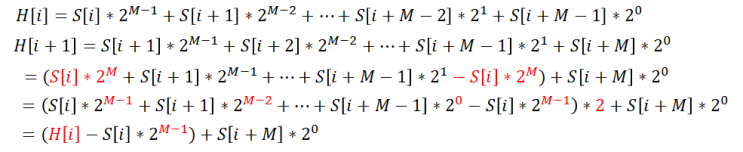
이것을 파이썬 코드로 구현해봤습니다.

T = input()
P = input()
len_t, len_p = len(T),len(P)
MOD = 2**28
powerlist = [2**n for n in range(28)]
power = powerlist[(len_p-1) % 28]

def mod(n):
    return n % MOD
def labin(pattern):
    res, j = 0, 0
    for i in range(len_p-1, -1, -1):
        res = mod(res+ord(pattern[i])*powerlist[j % 28])
        j += 1
    return res
def labin_wt_before(before,deleted,added):
    return mod(2*(before-ord(deleted)*power) + ord(added))

p_labin = labin(P)
res_count = 0
res_indices = ""

for idx in range(len_t-len_p+1):
    if idx == 0:
        t_labin = labin(T[:len_p])
    else:
        t_labin = labin_wt_before(before,T[idx-1],T[idx+len_p-1])
    before = t_labin
    if t_labin == p_labin:
        is_pattern = False
        for j in range(len_p):
            if P[j] != T[idx+j]:
                break
            if j == len_p-1:
                is_pattern = True
        if is_pattern:
            res_count += 1
            res_indices += f"{idx+1} "

print(res_count)
print(res_indices)